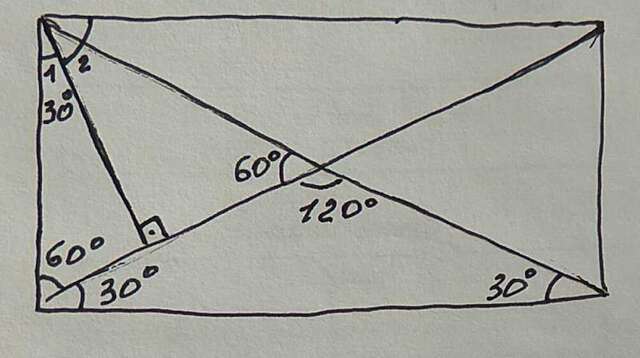
Перпендикуляр, опущенный к диагонали из прямого угла, образует два угла, один из которых составляет 1 часть, а другой - 2 части. В сумме прямой угол составляет 3 части, значит 90:3=30° Это меньший угол. В прямоугольном треугольнике, получившемся при проведении перпендикуляра, находим третий угол между стороной прямоугольника и его диагональю 180-(30+90)=60° Его смежный угол равен 90-60=30° В треугольнике, образованном стороной прямоугольника и его диагоналями, углы при основании равны, т. к. он равнобедренный. Угол при вершине этого треугольника равен 180-(30+30)=120° Находим искомый острый угол между диагоналями прямоугольника 180-120=60°