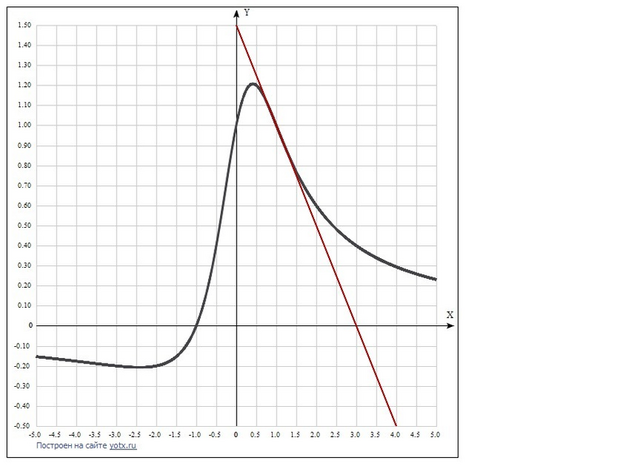
Уравнение касательной: y(кас) = y(хо)+y'(xo)*(x-xo).
Находим составляющие для хо = 1.
у(1) = (1+1)/(1+1) = 2/2 = 1.
y' = -(x²+2x-1)/(x²+1)².
y'(1) = -(1+2-1)/(1+1)² = -2/4 = -1/2.
Подставим в уравнение:
y(кас) = 1-(1/2)*(x-1) = -(1/2)х +1+(1/2) = -(1/2)х+(3/2).