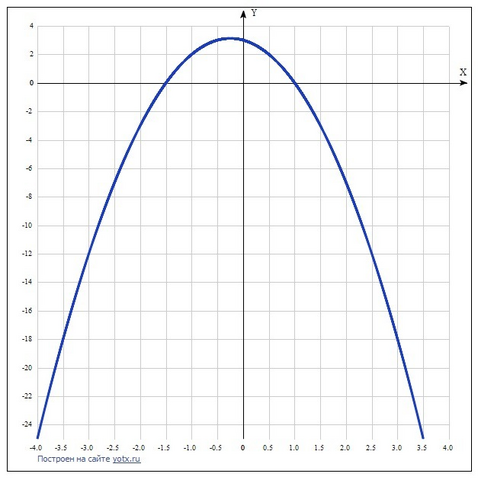
Дана функция y=-2x²-x+3.
График её - парабола ветвями вниз.
Находим координаты её вершины.
Хо = -в/2а = 1/(2*(-2)) = -1/4.
Уо = -2*(1/16) + (1/4) + 3 = 50/16 = 3,125.
Находим точки пересечения графиком оси Ох (при этом у = 0).
-2x²-x+3 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-1)^2-4*(-2)*3=1-4*(-2)*3=1-(-4*2)*3=1-(-8)*3=1-(-8*3)=1-(-24)=1+24=25;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=√25-(-1))/(2*(-2))=(5-(-1))/(2*(-2))=(5+1)/(2*(-2))=6/(2*(-2))=6/(-2*2)=6/(-4)=-6/4=-1.5;x₂=(-√25-(-1))/(2*(-2))=(-5-(-1))/(2*(-2))=(-5+1)/(2*(-2))=-4/(2*(-2))=-4/(-2*2)=-4/(-4)=-(-4/4)=-(-1)=1.Определим ещё несколько точек для построения графика.
x =
-4
-3 -2
-1 -0,25
0
1 2
3 4
y =
-25
-12 -3 2 3,125
3
0 -7 -18 -33.