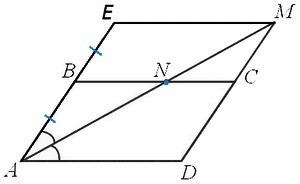
На прямой AB отложим отрезок AE равный DM.
AE=DM, AE||DM => AEMD - параллелограмм.
Если диагональ параллелограмма делит его угол пополам, то параллелограмм является ромбом. AE=AD =2AB
Точка B - середина AE, BC - средняя линия AEMD.
Средняя линия параллелограмма проходит через точку пересечения диагоналей (N). Диагонали параллелограмма точкой пересечения делятся пополам. AN=NM.
ИЛИ
∠BAN=∠NAD
∠BNA=∠NAD (накрест лежащие при BC||AD)
∠BAN=∠BNA => △ABN - равнобедренный, AB=BN
AB=AD/2 => BN=AD/2
BC=AD (противоположные стороны параллелограмма)
NC= BC-BN = AD -AD/2 =AD/2
NC - средняя линия △AMD (NC||AD, NC=AD/2) => AN=NM