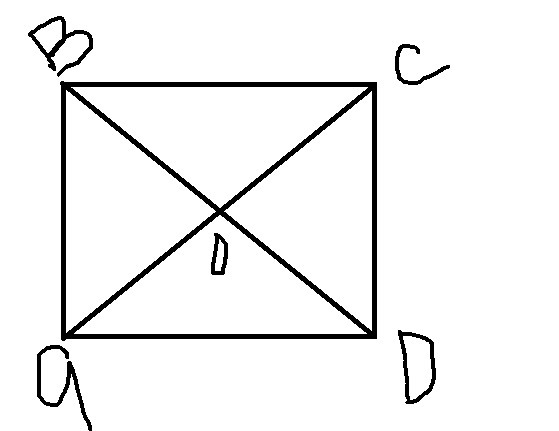
Дано: 4х-угольник АБСД. АС и БД - биссектрисы. Точка О является точкой их пересечения, и делит диагонали пополам, а значит БО = ОД, а АО = ОС. Если диагонали являются биссектрисами, то делят углы пополам, а сам 4х угольник на 4 треугольника.
Рассмотрим треугольники СОБ, АОБ, АОД и СОД. угол ОАД = углу ОДА, угол ОСД = углу ОДС, угол ОСБ = углу ОБС, угол ОБА = углу ОАБ. Исходя из всего этого можем сказать, что треугольники СОБ, АОБ, АОД и СОД - равнобедренные и равны между собой.
А так как они равны между собой, то и их основания БС, СД, АД и АБ - равны, а это значит, что АБСД - ромб