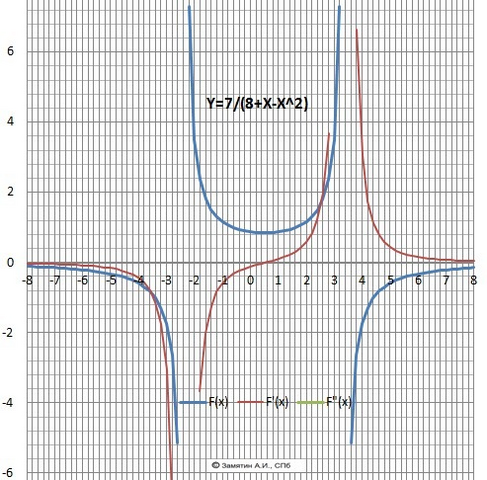
ДАНО Y= 7/(-x²+x+8)
ИССЛЕДОВАНИЕ
1. Область определения.
Решаем квадратное уравнение. D=33. Х1≈ -2,37, Х2 ≈ 3,37. Две точки разрыва.
D(x)∈(-∞;-2.37)∪(-2.37;3.37)∪(3.37;+∞).
Наклонные асимптоты - X≈ -2.37, X≈ 3.37
2.
Пересечение с осью Х - нет.
3. Пересечение
с осью У. У(0) = 7/8.
4. Поведение
на бесконечности.
limY(-∞) =0, limY(+∞) = 0.
Наклонная асимптота - Y = 0.
5. .Функция ни чётная ни нечётная.
6.
Производная функции.
Y'(x)= (14x-7)/(-x²+x+8)².
7. Корень при Х= 1/2 . Минимум – Ymin(0,5)=0,8485.
Возрастает
- Х∈(0,5;3,37)∪(3,37;+∞).
Убывает = Х∈(+∞;-2,37)∪(-2,37;0,5).
8. Точек перегиба - нет.
Выпуклая “горка» Х∈(-∞;-2,37)∪(3,37;+∞),
Вогнутая – «ложка» Х∈(-2,37;3,37).
9. График в
приложении.