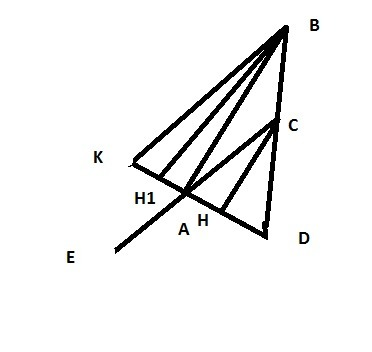
Из точек В и С опустим высоты ВН1 и СН. Треугольники ВН1А и САН подобны по двум углам (прямые углы при высотах и
ВА : АС=ВН1 :СН=ВD : CD(т.к. треугольники Н1BD и СНD тоже подобны по 2 углам)
ВА : АС = BD : CD , а значит BD : AB = CD : AC что и требовалось доказать...