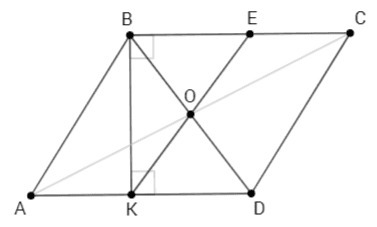
KB⊥BC, AD||BC => KB⊥AD, ∠BKD=90
BO=OD (диагонали параллелограмма точкой пересечения делятся пополам)
KO=OD (медиана, проведенная из вершины прямого угла, равна половине гипотенузы)
∠BEK=∠EKD, ∠EBD=∠BDK (накрест лежащие углы при AD||BC)
△BOE~△KOD (по двум углам)
BO/OD=OE/KO => BO=OE.
ИЛИ
Средняя линия параллелограмма (и лежащая на ней точка пересечения диагоналей) делит всякий отрезок, соединяющий противоположные стороны, пополам (по теореме Фалеса). Диагонали четырехугольника BEDK делятся точкой пересечения пополам => BEDK - параллелограмм. В параллелограмме BEDK угол KBE - прямой => BEDK - прямоугольник. Диагонали прямоугольника равны => равны их половины, BO=OE.