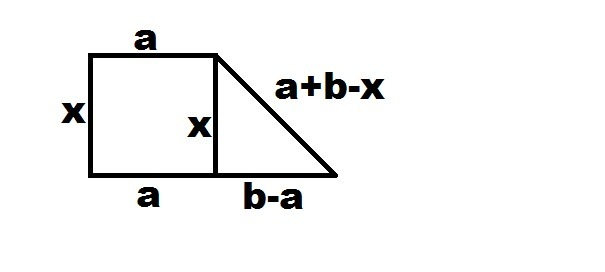Пусть меньшая боковая сторона равна x, тогда большая сторона, в силу того, что у четырехугольника, описанного около окружности, суммы противоположных сторон равны, равна: a + b - x
тогда по т. Пифагора:
(b-a)² = (a+b-x)² - x²
a² + b² - 2ab = a² + b² + 2ab + x² - 2(a+b)x - x²
4ab = 2(a+b)x
x = 2ab/(a+b)
(a+b-x) = ((a+b)² - 2ab)/(a+b) = (a²+b²)/(a+b)
Ответ: 2ab/(a+b), (a²+b²)/(a+b)