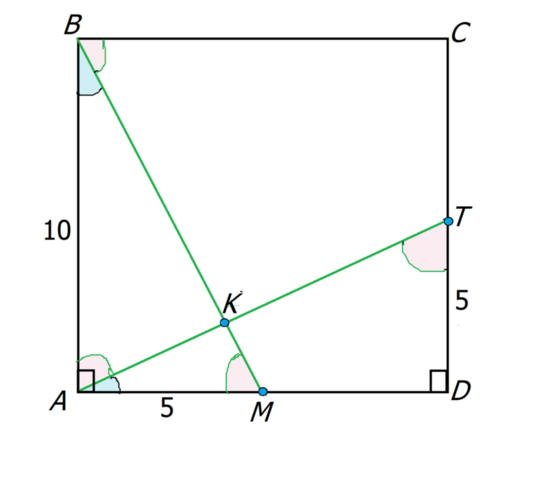
Рассмотрим приложенный рисунок.
Треугольники АВМ и АДТ равны по двум катетам.
Следовательно, все углы в них равны.
Из равенства углов этих треугольников следует, что треугольник АКМ прямоугольный, т.к. в нем острые углы равны острым углам прямоугольных треугольников.
Отсюда подобие треугольников АВМ и АКМ.
Коэффициент подобия треугольников найдем из отношения их гипотенуз.
k=ВМ:АМ
ВМ=√(АВ²+АМ²)=√125=5√5
Отношение площадей подобных фигур равно квадрату коэффициента их подобия. k=(5√5):5=√5
S(ABM):S (AKM)=k²=5
S(ABM)=10*5:2=25
S (AKM)=25:5=5