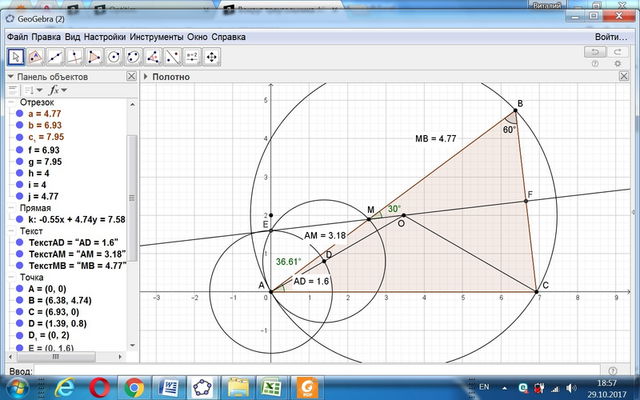
Диаметр и максимальная длина хорды заданной окружности равны 2*4=8.
Точка М принадлежит окружности с радиусом, равным (2/5)*4 = 1,6.
Угол ЕДА, как центральный, равен 2*30 = 60 градусов.
Поэтому прямая ОМ проходит через точку Е на оси ординат с координатами Е(0; 1,6).
Угол АОС равен 2*60 = 120 градусов.
Основание АС треугольника равно: АС = 2*4*cos 30° = 8*√3/2 = 4√3.
Тангенс угла наклона прямой ОМ равен:
tg KOE = (2-1.6)/(2√3) = 0.4/2√3 ≈ 0,11547.
∡KOE = arc tg
0,11547 =
0,114961 радиан = 6,586776°.
Тогда угол наклона стороны АВ к оси абсцисс равен:
∡А = 30° +
6,586776° =36,586776°.
∡С = 180° - 60° - 36,586776° =
83,41322°.
Теперь по стороне и двум углам находим и боковые стороны (по теореме синусов) и площадь треугольника АВС (по формуле Герона).
Известно:
сторона b и два прилегающих угла A и С.
Стороны b и с
равны :
а
b c
6,9282032 4,768316485 7,947194142
Угол А,градус 36,58678
Угол В,градус 60
Угол С,градус 83,413224
S =
16,40890239.