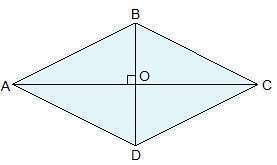
Ромб — это четырёхугольник, у которого все стороны равны. Ромб с прямыми углами называется квадратом.
Площадь ромба равна половине произведения его диагоналей:
S = (AC · BD) / 2.
Доказательство.
Пусть АВСD — ромб, АС и BD — диагонали.
Тогда SABCD = SABC + SACD = (AC · BO) / 2 + (AC · DO) / 2 = AC(BO + DO) / 2 = (AC · BD) / 2.
Что и требовалось доказать.
Так же площадь ромба можно найти с помощью следующих формул:
S = a · H, где a — сторона, H — высота ромба.
S = a2 · sin α, где α — угол между сторонами, a — сторона ромба.
S = 4r2 / sin α, где r — радиус вписанной окружности, α — угол между сторонами.