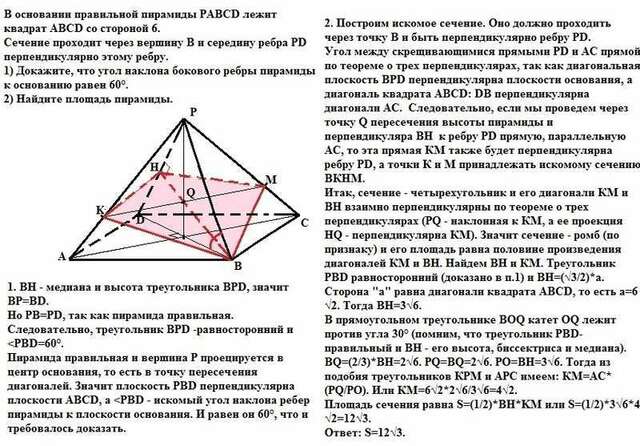
1. ВН - медиана и высота треугольника ВРD, значит ВР=BD.
Но РВ=PD, так как пирамида правильная.
Следовательно, треугольник ВРD -равносторонний и Пирамида правильная и вершина Р проецируется в центр основания, то есть в точку пересечения диагоналей. Значит плоскость РВD перпендикулярна плоскости АВСD, а
2. Построим искомое сечение. Оно должно проходить через точку В и быть перпендикулярно ребру PD.
Угол между скрещивающимися прямыми PD и АС прямой по теореме о трех перпендикулярах, так как диагональная плоскость BPD перпендикулярна плоскости основания, а диагональ квадрата АВСD: DB перпендикулярна диагонали АС. Следовательно, если мы проведем через точку Q пересечения высоты пирамиды и перпендикуляра ВН к ребру PD прямую, параллельную АС, то эта прямая КМ также будет перпендикулярна ребру PD, а точки К и М принадлежать искомому сечению ВКНМ.
Итак, сечение - четырехугольник и его диагонали КМ и ВН взаимно перпендикулярны по теореме о трех перпендикулярах (PQ - наклонная к КМ, а ее проекция НQ - перпендикулярна КМ). Значит сечение - ромб (по признаку) и его площадь равна половине произведения диагоналей КМ и ВН. Найдем ВН и КМ. Треугольник РВD равносторонний (доказано в п.1) и ВН=(√3/2)*а.
Сторона "а" равна диагонали квадрата АВСD, то есть а=6√2. Тогда ВН=3√6.
В прямоугольном треугольнике ВОQ катет ОQ лежит против угла 30° (помним, что треугольник РВD- правильный и ВН - его высота, биссектриса и медиана).
ВQ=(2/3)*ВН=2√6. PQ=BQ=2√6. РО=ВН=3√6. Тогда из подобия треугольников КРМ и АРС имеем: КМ=АС*(PQ/РO). Или КМ=6√2*2√6/3√6=4√2.
Площадь сечения равна S=(1/2)*BH*KM или S=(1/2)*3√6*4√2=12√3.
Ответ: S=12√3.