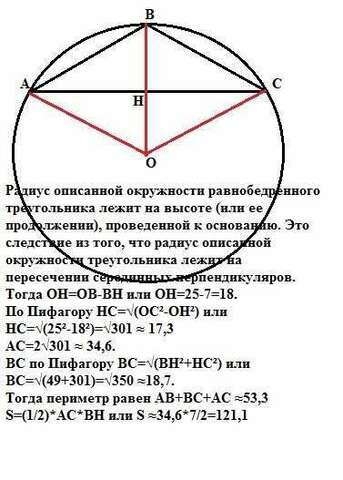
Радиус описанной окружности равнобедренного треугольника лежит на высоте (или ее продолжении), проведенной к основанию. Это следствие из того, что радиус описанной окружности треугольника лежит на пересечении серединных перпендикуляров.
Тогда ОН=ОВ-ВН или ОН=25-7=18см.
По Пифагору НС=√(ОС²-ОН²) или
НС=√(25²-18²)=√301 ≈ 17,3см.
АС=2√301 ≈ 34,6см.
ВС по Пифагору ВС=√(ВН²+НС²) или
ВС=√(49+301)=√350 ≈18,7см.
Тогда периметр равен АВ+ВС+АС ≈53,3см
S=(1/2)*AC*BH или S ≈34,6*7/2=121,1см².