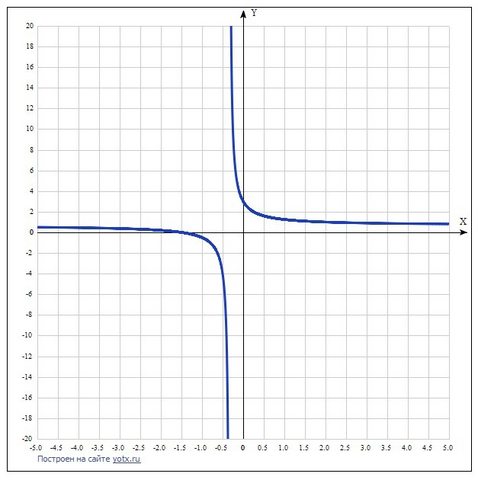
Дана функция у=(2x+3)/(3x+1).
Функции не решаются, а показывают зависимость переменной у от независимой переменной х.
Чтобы наглядно увидеть эту зависимость, строят график: принимают несколько значений х и рассчитывают значение у.
x = -3 -2 -1 0 1 2 3
y = 0,375 0,2
-0,5
3 1,25 1 0,9.
Наносим точки на график и соединяем плавной линией.
1) Точки, в которых функция точно не определена: переменная в знаменателе, 3х + 1 ≠ 0, х ≠ -1/3.
2) График функции пересекает ось X при f = 0
значит надо решить уравнение:
\frac{2 x + 3}{3 x + 1} = 0
Точка пересечения с осью X: 2х + 3 = 0, х = -3/2.
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в (2*x + 3)/(3*x + 1).
Получаем 3/1 = 3.
Точка: (0, 3).
3) Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
\frac{2 x + 3}{3 x + 1} = \frac{- 2 x + 3}{- 3 x + 1}
- Нет
\frac{2 x + 3}{3 x + 1} = - \frac{- 2 x + 3}{- 3 x + 1}
- Нет, значит, функция не является ни чётной, ни нечётной.
4) Анализ на экстремумы и точки перегиба для данной функции не производим, так как они отсутствуют - функция является гиперболой.
5) Есть 2 асимптоты: одна вертикальная в точке разрыва функции х = -1/3, вторая - горизонтальная, является пределом функции при х стремящемся к (-1/3) - это у = 2/3.
6) Исследование на монотонность.
Находим производную функции.
y' = -7/(3x+1)². Видим, что производная на всей области определения отрицательна, значит, функция убывающая.