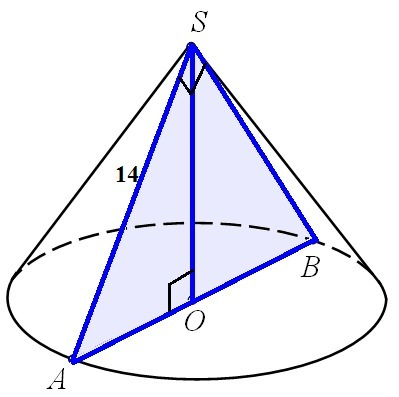
Осевым сечением конуса является прямоугольный треугольник SAB, где:
Образующие AS = BS = 14 cм ⇒ треугольник SAB является равнобедренным с углом 90° при вершине, основанием AB, равным диаметру окружности основания конуса.
Высота (SO) конуса является высотой равнобедренного треугольника SAB, проведенной к основанию AB (а также медианой и биссектрисой) ⇒ SO делит угол при вершине треугольника SAB пополам ⇒ ∠ASO = ∠BSO = 45°
В прямоугольном треугольнике ASO:
∠ASO = 45°
∠AOS = 90°
∠SAO = 180 - 90 - 45 = 45 (°)
⇒ треугольник ASO является прямоугольным равнобедренным с основанием AS, боковыми сторонами AO = SO = r
Радиус окружности основания конуса равен высоте конуса.
Найдем AO через косинус угла SAO. Косинусом угла SAO является отнрошение прилежащего к нему катета AO к гипотенузе AS
AO
cos(SAO) = ---------------
AS
AO
cos(45°) = ---------------
14
AO 1
--------- = ----------
14 √2
AO * √2 = 14 * 1
AO = 14/√2
r = 14/√2 (см)
Площадь основания конуса равна:
S = π * r²
S = π * (14/√2)² = π * 196/2 = 98π ≈ 308 (cм²)