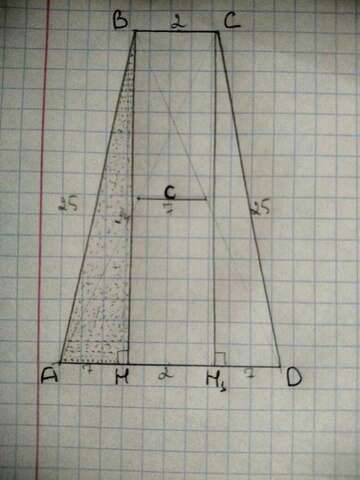
С вас: оценить мой ответ в 5 звезд, а с меня - решение. Погнали.
c =

- по свойству равнобедренной трапеции, тогда 2c=AD-BC⇒BC=AD-2c⇒BC=2 (см)
Поскольку BH⊥AD=C

⊥AD - как высоты, AB=CD - как стороны равнобедренной трапеции, то ΔАВН=Δ

СD - по гипотенузе и катету, а HBC

- прямоугольник по определению, и по его свойству: ВС=Н

=2 (см)
Значит AH=

D=

=7 (см)
В ΔАВН по теореме Пифагора: BH=

= 24(см)

=
216(см )
)