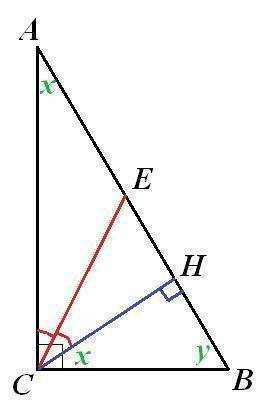
Обозначим в ΔАВС углы х=∠А, у=∠В.
Выразим другие углы через х и у.
Т.к. ∠А и ∠В - острые углы прямоугольного ΔАВС, то ∠А+∠В=90°, поэтому х=90°-у.
Аналогично, ∠НСВ и ∠В - острые углы прямоугольного ΔНВС, тогда ∠НСВ+∠В=90°, поэтому ∠НСВ=90°-∠В=90°-у = х.
Т.к. ∠АСВ=90°, то ∠АСН=90°-х.
Т.к. СЕ - биссектриса ∠АСН, то ∠АСЕ=∠НСЕ=
Рассмотрим ΔЕСВ. У него:
∠ЕСВ = ∠СНЕ+∠НСВ = 
Рассмотрим ΔЕСН. У него:
∠СЕН = 90°-∠НСЕ = 
Итак, получили в ΔЕСВ ∠ЕСВ=∠СЕВ=
Значит, ΔЕСВ - равнобедренный с основанием СЕ. Значит, ВЕ=ВС.
Доказано.