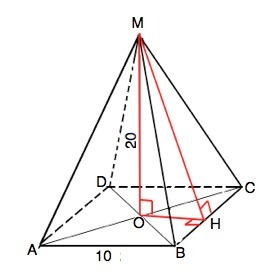
(Поскольку о ребрах пирамиды ничего не говорится, примем допущение, что она правильная, тогда все ее грани равны, а вершина проецируется в центр основания.)
Площадь полной поверхности пирамиды - сумма площади основания и площади боковой поверхности.
S=S(ABCD)+4•S(∆ MBC)
Проведем ОН ⊥ ВС.
Углы основания прямые, поэтому ОН║АВ.
О - центр (АВСD) ⇒ ОН=АВ:2=5 см
S ∆ MBC=0,5MH•BC
Проведем МН. По т. о 3-х перпендикулярах МН⊥ВС. ⇒
МН - высота ∆ ВМС.
МН=√(MO²+HO²)=√(400+25)=5√17
S(полн)=10²+4•0,5•10•5√17=100+100•5√17=100(1+5√17) см²