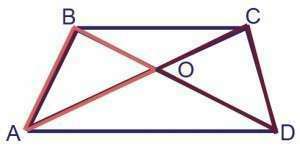
Можно провести из точки С прямую II ВD и продлить AD до пересечения с этой прямой, пусть это точка Е. Треугольник АВЕ имеет ту же площадь, что и трапеция, потому что его оcнование равно (AD + BC), а высота у них общая - расстояние от С до AD.
Треугольник АВЕ подобен АDО, и отношение сторон (3 + 4)/4 = 7/4; значит отношение площадей (7/4)^2 = 49/16, осталось заметить, что площадь треугольника ADO равна 4/3 от площади треугольника АВО, потому что ВО = OD*3/4, а высота этих треугольников общая - это расстояние от А до BD.
Итак, площадь ADO = 6*4/3 = 8;
S = 8*49/16 = 49/2;
ПОСТАВЬ ОЦЕНКУ ПЛЕС