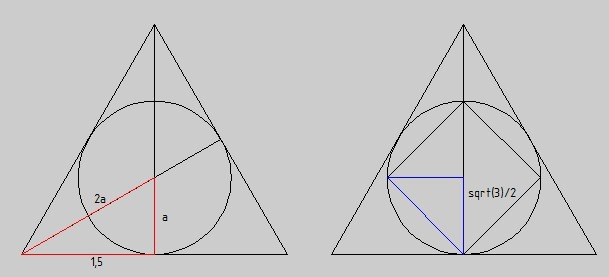
Из красного прямоугольного треугольника на рисунке найдём радиус вписанной окружности, т.к. его острый угол равен 30°
![(2a)[tex]S=(\frac{ \sqrt{3} }{2})^{2}+(\frac{ \sqrt{3} }{2})^{2}=\frac{6}{4}=\frac{3}{2} (2a)[tex]S=(\frac{ \sqrt{3} }{2})^{2}+(\frac{ \sqrt{3} }{2})^{2}=\frac{6}{4}=\frac{3}{2}](https://tex.z-dn.net/?f=+%282a%29%5Btex%5DS%3D%28%5Cfrac%7B+%5Csqrt%7B3%7D+%7D%7B2%7D%29%5E%7B2%7D%2B%28%5Cfrac%7B+%5Csqrt%7B3%7D+%7D%7B2%7D%29%5E%7B2%7D%3D%5Cfrac%7B6%7D%7B4%7D%3D%5Cfrac%7B3%7D%7B2%7D) =a^{2}+(\frac{3}{2})^{2}\\
3a^{2}=\frac{9}{4}\\
a=\frac{ \sqrt{3} }{2}[/tex]
=a^{2}+(\frac{3}{2})^{2}\\
3a^{2}=\frac{9}{4}\\
a=\frac{ \sqrt{3} }{2}[/tex]
теперь из синего треугольника найдём квадрат его гипотенузы, который и равен площади вписанного квадрата