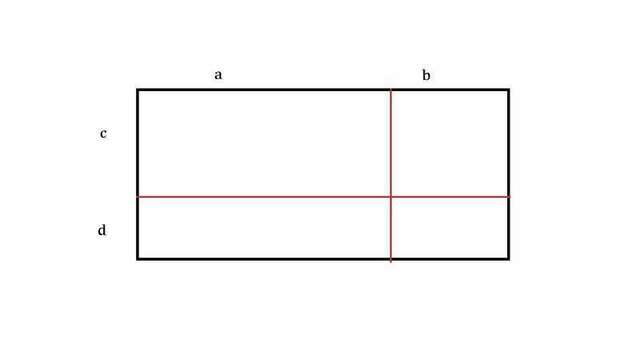
Разделим прямоугольник как показано на рисунке.
Пусть одна сторона прямоугольника разбита на отрезки a и b.
Прилежащая сторона разбита на отрезки c и d.
По условию:
bc=30
ad=50
ac=60
2bc=60
ac=60
2bc=ac
b=0.5а
a=50/d
a=60/c
50/d=60/c
c=60/50d
c=1.2d
Общая площадь всего прямоугольника равна:
S=(a+b)(c+d)=(0,5а+а)(d+1.2d)=1,5а*2.2d=3,3ad=3.3*50=165 площадь исходного прямоугольника
Ответ 165