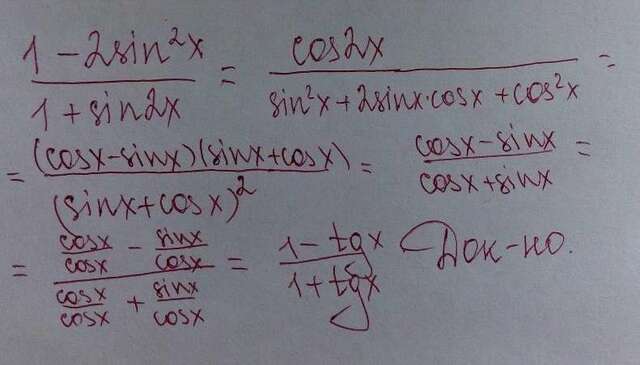Для доказательства данного тождества необходимо и достаточно знать несколько формул:
1) cos2x = 1 - 2sin^2(x) = cos^2(x) - sin^2(x) = (cosx - sinx) * (cosx + sinx);
2) sin2x = 2sinx*cosx;
3) 1 = sin^2(x) + cos^2(x);
4) 1 + sin2x = sin^2(x) + cos^2(x) + 2sinx*cosx = (sinx + cosx)^2 (выделение полного квадрата).
В ходе решения получаем дробь: (cosx - sinx)/(cosx + sinx). Числитель и знаменатель делим на cosx, откуда и получаем заветную правую часть тождества.