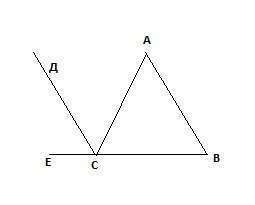
Построим треугольник
АВС удовлетворяющий условию задачи (угол АСЕ – внешний угол, СД – биссектриса угла
АСЕ, ДС||АВ).
Так как ДС||АВ при АС –
секущей, то по Теореме об углах,
образованных двумя параллельными прямыми и секущей:
углы АСД=ВАС – как накрест
лежащие.
Углы ДСЕ=АВС – как соответственные.
Но, так как углы
АСД=ДСЕ (так как СД – биссектриса), то и углы ВАС=АВС.
У равнобедренного
треугольника углы при основании равны, значит, треугольник АВС является равнобедренным
(АВ – основание, АС = ВС – боковые стороны)