Как я понимаю, нельзя просто преобразовать выражения и показать их равенства, а надо долго и пространно рассуждать.
Итак, пусть х ∈ A\B (это кстати просто разность множеств, не симметрическая). Тогда из свойств операций над множествами верно, что х ∈ А ∩ -B (буду обозначать отрицание минусом). Теперь посмотрим на правую часть. Пусть х ∈ А\(А∩В), отсюда опять же верно, что х ∈ А ∩ х ∈ -(А∩В), или же по закону де Моргана х ∈ А ∩ х ∈ -А∪-В, или же х ∈ А ∩ (х ∈ -А ∪ х ∈ -В), или же по принципу дистрибутивности (х ∈ А ∩ х ∈ -А) ∪ (х ∈ А ∩ х ∈ -В), и отсюда наконец по принципу дополнения х ∈ ∅ ∪ х ∈ А ∩ -В, и по свойству нуля х ∈ А ∩ -В. Как мы видим, левая часть в этом смысле идентична правой. То есть в принципе уже равенство верно. Наверное, предполагается, что сначала надо из левой части вывести правую, а потом наоборот. Тут надо будет просто продолжить этот ряд операций в другую сторону, если действительно надо.
2) Метод, конечно, какая-то жесть в смысле записи, поэтому я просто преобразую левую часть в правую и потом наоборот как логические выражения без упоминания ссылок на конкретные свойства.
A\(B\C)=(A\B)\/(A/\C)
Работаем с левой частью:
A\(B\C) = А ∩ -(В\С) = А ∩ -(В∩-С) = А ∩ (-В ∪ С) = (А ∩ -В) ∪ (А ∩ С) = (А\В) ∪ (А ∩ С) - вывели правую. Из правой левую - повторяем всю цепочку действий, но наоборот.
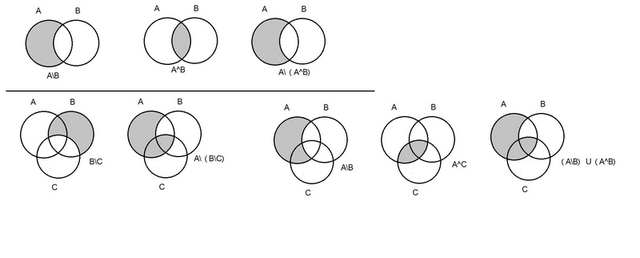
А в конце для проверки диаграммы.