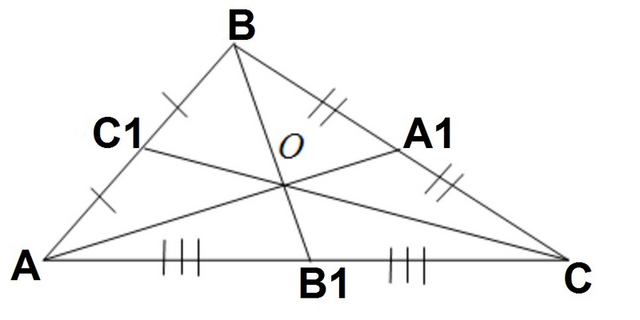
Медианы треугольника пересекаются в точке О, которая делит каждую медиану в отношении 2:1 считая от вершины (свойство).
AO составляет 2/3 от 3, ОА1 составлят 1/3 от 3.
АО = 2. ОА1 = 1
СО составляет 2/3 от 12, ОС1 составляет 1/3 от 12
СО = 8. OC = 4
Найдем площадь треугольника AOC по формуле Герона:
S = 
p = (a + b + c) / 2
p(AOC) = (AO + CO + AC) / 2
p(AOC) = (2 + 8 + 7) / 2 = 17 / 2
S(AOC) =  =
=  =
=  =
=  (кв. ед)
(кв. ед)
Треугольник делится тремя медианами на шесть равновеликих треугольников (свойство) ⇒ S(ABC) = 3 * S(AOC)
S(ABC) =  =
=  (кв. ед)
(кв. ед)
-----------------------------------------------------------------------------------------------
Площадь треугольника AOB1 равна половине площади треугольника AOC.
S(AOB1) = S(AOC) / 2
S(AOB1) =  (кв. ед)
(кв. ед)
p(AOB1) = (AO + OB1 + AB1) / 2
AB1 = AC / 2
AB1 = 7/2
OB1 = x
p(AOB1) = (2 + x + 7/2) / 2
p (AOB1) =  =
= 
S(AOB1) = 
 =
= 

Возводим обе части уравнения в квадрат
 =
= 
Умножаем обе части уравнения на 256
(121 - 4x²)(4x² - 9) = 2652
484x² - 16x⁴ - 1089 + 36x² - 2652 = 0
-16x⁴ + 520x² - 3741 = 0
x² = t
ОДЗ t > 0, т.к. результат возведения в четную степень не может быть отрицательным и длина не может быть равной нулю
-16t² + 520t - 3741 = 0
16t² - 520t + 3741 = 0
D = (-520)² - 4 * 16 * 3741 = 270400 - 239424 = 30976
√D = 176
t1 = (520 + 176) / 32 = 696/32 = 21,75
t2 = (520 - 176) / 32 = 344/32 = 10,75
Оба корня отвечают ОДЗ
X1 = √21,75
X2 = √10,75
BB1 = OB1 * 3
1) OB1 = √21,75, тогда BB1 = 3√21,75
2) OB1 = √10,75, тогда BB1 = 3√10,75
При подстановке обоих вариантов в формулу Герона для треугольника AOB1 получается одинаковая площадь
(Рисунок схематический)