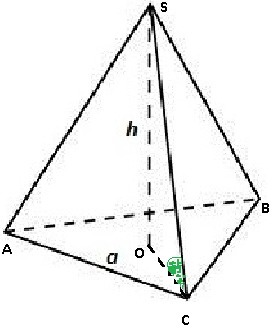
Задание. Боковое ребро правильной треугольной пирамиды равно 10 и наклонено к плоскости основания под углом 30º. Найти объем пирамиды.
Решение:
∠SCO = 30°. Рассмотрим прямоугольный треугольник SOC. Против угла 30° катет в 2 раза меньше за гипотенузу, т.е.

.
 OK - радиус описанной окружности, т.е.
OK - радиус описанной окружности, т.е. 
- сторона основания.
Найдем теперь площадь основания:

Окончательно вычислим объем пирамиды:
 Ответ:
Ответ: