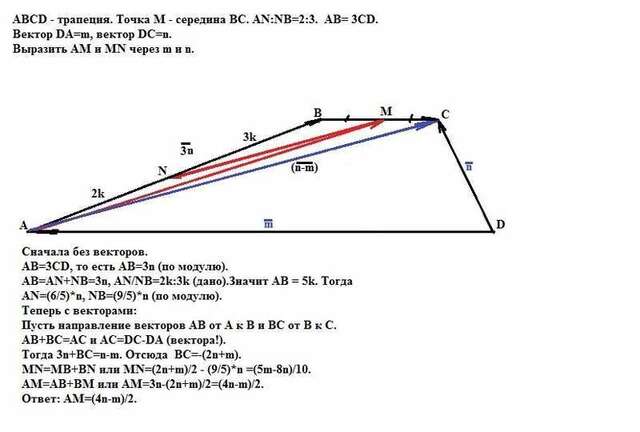
АВСD - трапеция. Точка М - середина ВС. AN:NB=2:3. AB= 3СD.
Вектор DA=m, вектор DC=n.
Выразить AM и MN через m и n.
Сначала без векторов.
АВ=3CD, то есть АВ=3n (по модулю).
АВ=AN+NB=3n, AN/NB=2k:3k (дано).Значит АВ = 5k. Тогда
AN=(6/5)*n, NB=(9/5)*n (по модулю).
Теперь с векторами:
Пусть направление векторов АВ от А к В и ВС от В к С.
АВ+ВС=АС и АС=DC-DA (вектора!).
Тогда 3n+BC=n-m. Отсюда ВС=-(2n+m).
MN=MB+BN или MN=(2n+m)/2 - (9/5)*n =(5m-8n)/10.
АМ=АВ+ВМ или АМ=3n-(2n+m)/2=(4n-m)/2.
Ответ: AM=(4n-m)/2.