1.

2.

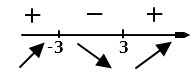
Получили 2 критических точки, теперь нужно проверить, меняет ли производная свой знак, при прохождении через эти точки. При прохождении x = -3, знак меняется с плюса на минус, значит, х=-3 - максимум, при прохождении х = 3, знак меняется с минуса на плюс, значит, х = 3 - минимум