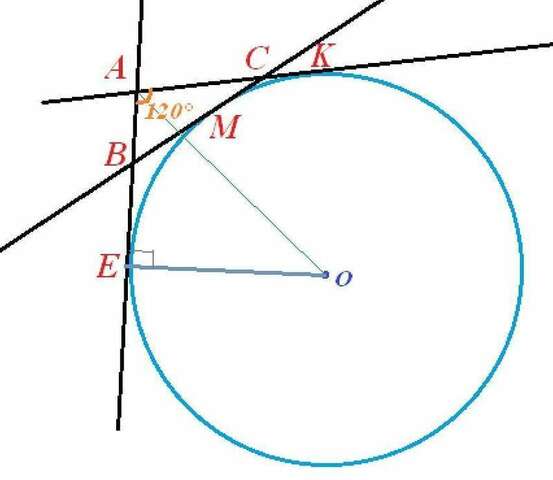
Пусть О - центр окружности. Рассмотрим ΔАВС, ∠А=120°, P Δ = 10. Требуется найти длину отрезка АО.
Отметим точки касания окружности:
Е - точка касания окружности и продолжения АВ,
М - точка касания окружности и ВС,
К - точка касания окружности и продолжения АС.
По свойству отрезков касательных к окружности, проведенных из одной точки: ВЕ=ВМ, СМ=СК. Тогда Р ΔАВС = АВ+ВС+АС = АВ+ВМ+СМ+АС=
= АВ+ВЕ+АС+СК = АЕ+АК.
По тому же свойству отрезков касательных к окружности, проведенных из одной точки: АЕ = АК.
Таким образом, P ΔABC = 2AE
Значит, АЕ=АК=10:2=5
Окружность с центром О является вневписанной для ΔАВС. Следовательно, ее цент лежит на биссектрисе ∠ ЕАК.
АО - биссектриса ∠ ЕАК. Тогда в ΔАЕО ∠ЕАО = 60°.
По свойству касательной к окружности и ее радиуса, проведенного в точку касания ОЕ⊥АЕ. Значит, ΔАОЕ - прямоугольный и ∠АОЕ=30°.
Катет АЕ, лежащий против угла в 30° в 2 раза меньше гипотенузы АО.
Значит АО = 2·5=10.
Ответ: 10.