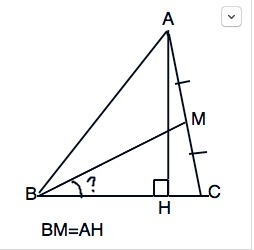
В треугольнике АВС проведена медиана ВМ и высота АН. Известно, что МВ=АН. Найдите величину угла МВС.
ВМ, как медиана, делит ∆ АВС на два равновеликих. ⇒
Ѕ ∆ АВМ=Ѕ ∆ ВМС⇒
Ѕ (∆ АВС)=2•Ѕ(∆ МВС)
Одна из формул площади треугольника
S=a•b•sinα, где а и b – стороны треугольника, α –угол между ними. ⇒
Ѕ (∆АВС)=2•0,5BM•BC•sinMBC
По другой формуле
Ѕ(∆ АВС)=0,5АН•ВС
Приравняем оба уравнения:
2•0,5BM•BC•sinMBC=0,5АН•ВС
Сократив одинаковые множители, получим
2•BM•sinMBC=АН
Так как ВМ=АН то
2•sinMBC=1 ⇒
sin MBC=0,5⇒угол МВС=30°
-------------------
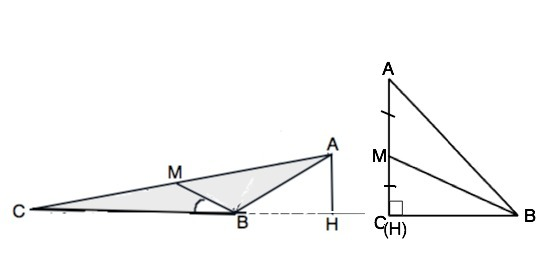
Решение подходит как для остроугольного, так и для тупоугольного треугольника. Для прямоугольного тоже, но тогда Н совпадает с вершиной С