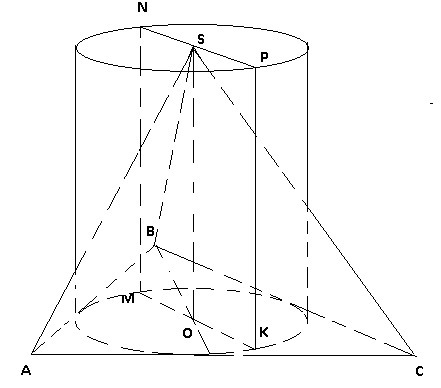
Задание. В основании пирамиды лежит правильный треугольник. В него вписана окружность, являющаяся основанием цилиндра той же высоты, что и пирамида. Найдите объём пирамиды, если объём цилиндра равен п корень из 3.
Решение:

Объем цилиндра равен: 
, а объем пирамиды:

, где Sо - площадь основания.
Поработаем немного над площадью основанием пирамиды. Поскольку в основе лежит правильный треугольник, то площадь основания равен

. В правильный треугольник вписан окружность, т.е.

откуда

. Подставив сторону основания в площадь основания пирамиды, получим

По условию, объем цилиндра равен π√3, т.е.

откуда

.
Находим теперь объем пирамиды:
 Ответ: Vпирамиды = 3.
Ответ: Vпирамиды = 3.