1) y=x²-2x+3;
Находим производную функции:
y'=(x²-2x+3)'=2x-2;
Приравниваем производную к нулю:
2х-2=0;
2x=2;
x=1.
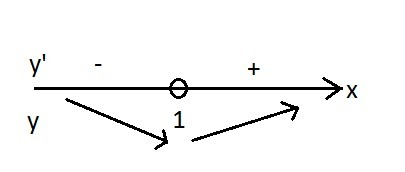
В точке х=1 функция имеет экстремум.
На промежутке (-∞;1) производная y'<0, <br>на промежутке (1;+∞) производная y'>0.
Значит, на промежутке (-∞;1) функция спадает,
на промежутке (1;+∞) функция возрастает.
5) Находим производную функции:
y'=(-9/x-x)'=9/x²-1.
Приравниваем производную к нулю:
9/x²-1=0;
9/x²=1;
x²=9;
x=+-3.
В точках -3 и 3 функция имеет экстремумы.
К промежутку [1;4] относится х=3.
Находим значение функции функции в точках х=1, х=3, х=4.
f(1)=-9/1-1=-9-1=-10 - наименьшее значение функции;
f(3)=-9/3-3=-3-3=-6 - наибольшее значение функции;
f(4)=-9/4-4=-2,25-4=-6,25.