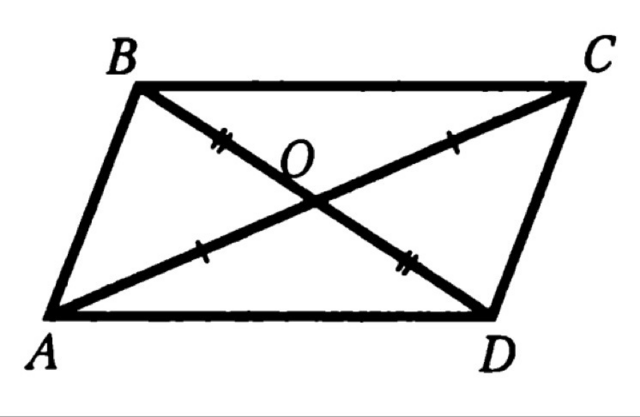
Доказательство: боковые треугольники равны по двум сторонам и углу между ними (BO = OD — по условию, AO = OC — по условию, ∠DOC = ∠AOB — вертикальные), то есть ∠ACD = ∠CAB, а поскольку они являются накрест лежащими при прямых AB, CD и секущей AC, то AB параллельна DC. Аналогично доказываем параллельность прямых BC и AD. Итак, ABCD — параллелограмм по определению. BC = AD, AB = CD (в параллелограмме противоположные стороны равны), AC — общая для треугольников ACD и CAB, поэтому они равны по трем сторонам. Что и требовалось доказать.