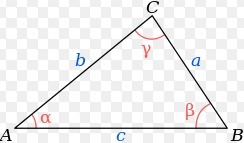
Задание. Основание треугольника равна 20,а медианы проведенные к боковым сторонам равны 18 и 24.Найти площадь треугольника.
Решение:
Пусть 
, а медианы проведенные к боковым сторонам

Медиана проведенная к стороне с равна:

.
Найдем боковые стороны


По т. Косинусов

тогда

Радиус описанной окружности(обобщенная теорема синусов):

.
Найдем площадь треугольника:
 Ответ: 288.
Ответ: 288.