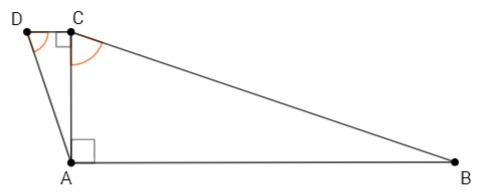
CA⊥AB, AB||CD => CA⊥CD
∠CAB=90°, ∠DCA=90°
∠DCB+∠DAB=270° <=> ∠DCA+∠ACB+∠DAC+∠CAB=270° <=> ∠ACB+∠DAC=90°
∠CDA+∠DAC=90° (сумма острых углов прям. треугольника равна 90°)
∠ACB=∠CDA
△ACB~△CDA (по двум углам)
CD/AC=CA/AB=AD/BC
CD/AB=1/9 <=> CD= AB/9
CD/AC=CA/AB <=> CD= CA^2/AB
AB/9= CA^2/AB <=> (CA/AB)^2 =1/9 <=> CA/AB=1/3
AD/BC=CA/AB=1/3