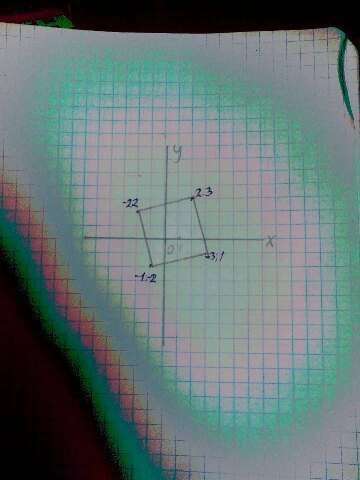
Найдем координаты середин диагоналей четырехугольника: середины ac х=(3-2)/2=0.5 y=(-1+2)/2=0.5 (0.5;0.5) середины BD х=(2-1)/2=0.5 y=(3-2)/2=0.5 Таким образом диагонали четырехугольника пересекаются в точке, что делит их пополам, поэтому за признаком парарлеллограмма четырехугольник АВСD - парареллограмм. Найдем длины диагоналей AC=((-2-3)^2+(-1-2))^2=(-5)^2+(-3)^2=25+9=34 BD=((2+1)^2+(3+2))^2=9+25=34 Диагонали параллелограма ABCD равны АC=BD, за признаком прямоугольника ABCD- прямоугольник. Доказано