Спільна хорда двох кіл, які перетинаються, є стороною правильного трикутника, вписаного в...

Question

Спільна хорда двох кіл, які перетинаються, є стороною правильного трикутника, вписаного в одне коло, і стороною квадрата, вписаного в інше коло. Довжина цієї хорди дорівнює a. Знайдіть відстань між центрами кіл, якщо вони лежать по різні сторони хорди.

Comments

Ответ дан, но запаздывает, проявится через несколько минут

Answer 1

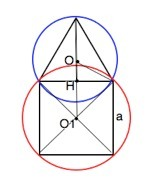
Общая хорда двух  пересекающихся кругов является стороной правильного треугольника, вписанного в один круг, и стороной квадрата, вписанного в другой круг. Длина этой хорды равна a. Найдите расстояние между центрами окружностей, если они лежат по разные стороны хорды. 

            Обозначим центр окружности с вписанным треугольником О, центр второй - О1. 

Стороны треугольника и квадрата равны а. 

Искомое расстояние равно сумме  расстояний ОН -  от точки пересечения медиан треугольника,-  до хорды-  и  НО1 - от хорды до точки пересечения диагоналей квадрата.

ОН равно радиусу окружности,  вписанной в правильный треугольник, т.е.1/3 его высоты. 

Высота =а√3/2. ОН= а√3/6 

Расстояние от хорды до О1 равно половине стороны квадрата, т.е. 

НО1=а/2 

---