В треугольнике АВС известно,что угол С=90°. угол В=30°. На катете ВС отметили точку D...

4.
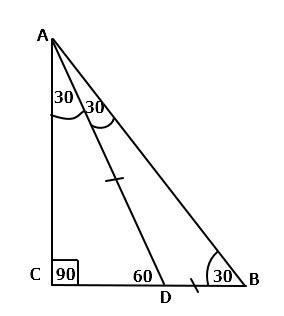
Дано: ΔABC, ∠C = 90°, ∠B = 90°, ∠ADC = 60°, CD = 5 см
Найти: BC
Решение:
Проведём AD.
Рассмотрим ΔCAD: ∠C = 90° (по усл), ∠ADC = 60° (по усл) ⇒
∠CAD = 180° - (90° + 60°) = 30°
Рассмотрим ΔABC: ∠C = 90° (по усл), ∠B = 60° (по усл) ⇒ ∠A = 180° - (90° + 30°) = 60°
∠C = ∠CAD + ∠DAB ⇒ ∠DAB = ∠C - ∠CAD = 60° - 30° = 30°
Рассмотрим ΔADB: ∠B = 30° (по усл), ∠DAB = 30° ⇒ ΔADB - равнобедренный, поэтому AD = DB
Вернёмся к ΔCAD, по теореме синусов получаем:
$\frac{CD}{sin CAD}= \frac{AD}{sinC} \Rightarrow\\ \frac{5}{sin30}= \frac{AD}{sin90} \Rightarrow\\ \frac{5}{ \frac{1}{2} }= \frac{AD}{1} \Rightarrow\\ AD = 10$
Т.к. AD = DB ⇒ 10 см
CB = CD + DB = 5 см + 10 см = 15 см

В треугольнике АВС известно,что угол С=90°. угол В=30°. ** катете ВС отметили точку D...