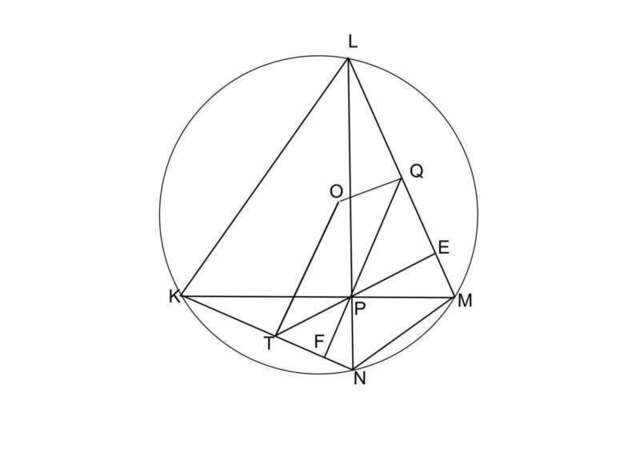
Мне понравился мой рисунок, так что я, пожалуй, сделаю исключение для этой задачки.
Пусть O - центр окружности, а Т - середина KN, и PT пересекает LM в точке E. Так как треугольник KPT
равнобедренный, есть такая "цепочка" равных углов ∠PLM = ∠PKN = ∠KPT =
∠EPM; откуда ясно, что в треугольнике LMP PE - высота.
То есть - другими словами - получилось, что если через точку P пересечения диагоналей провести прямую перпендикулярно LM, то она пройдет через середину KN - точку T;
Точно так же через точку P можно провести прямую перпендикулярно KN, и
она пройдет через середину LM - точку Q.
Легко видеть, что OQPT -
параллелограмм. Так как OQ тоже перпендикулярно LM, а OT перпендикулярно KN.
То есть OQ II PT; OT II PQ;
Следовательно OT = PQ = LN/2; (PQ - медиана прямоугольного треугольника LMQ)