1.
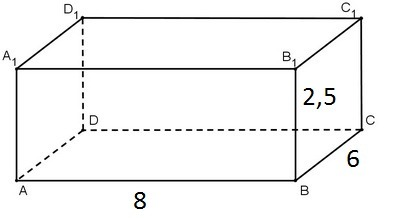
1) Пусть ABCDA1B1C1D1 - прямоугольный параллелепипед, АВ=8 м, ВС=6 м, ВВ1=2,5 м.
Sбок=Pосн*h=2*(АВ+ВС)*ВВ1=2*(8+6)*2,5=2*14*2,5=70 (м²).
2) Находим количество рулонов:
70:5=14 (рулонов).
Ответ: 14 рулонов.
2.
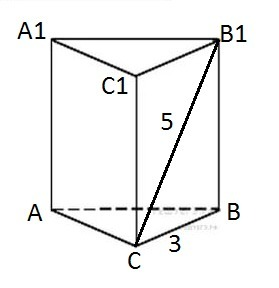
1) Пусть АВСА1В1С1 - правильная треугольная призма, ВС=3 м, СВ1=5 м. Площадь полной поверхности можно найти по формуле:
Sполн=Sбок+2Sосн.
2) Площадь боковой поверхности находим по формуле:
Sбок=P*h=3*ВС*ВВ1.
Рассмотрим ΔСВВ1 - прямоугольный, по т. Пифагора
ВВ1=√(СВ1²-СВ²)=√(5²-3²)=√(25-9)=√16=4 (м).
Sбок=P*h=3*ВС*ВВ1=3*3*4=9*4=36 (м²).
3) Так как основание призмы правильный треугольник, то его площадь находим по формуле:
S=a²√3/4=ВС²√3/4=3²√3/4=9√3/4 (м²).
4) Sполн=Sбок+2Sосн=36+2*9√3/4=36+9√3/2=9(4+√3/2) (м²).
Ответ: 9(4+√3/2) м².