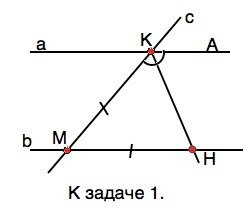
1) Прямые a и b пересекаются прямой с (см. рисунок приложения).
МК=МН, а КН делит внутренний угол АКМ пополам,
∆ КМН - равнобедренный по условию, поэтому углы при его основании КН равны.
Из равенства углов АКН и НКМ следует равенство накрестлежащих углов КНМ, и НКА, Если накрестлежащие углы при пересечении двух прямых секущей равны, прямые параллельны. Доказано.
* * *
2) В прямоугольном треугольнике АВС с прямым углом С проведена биссектриса АD. Угол САD=20°. Найти угол В.
---------
Т.к. АD биссектриса, полный угол А=2•20°=40°.
Сумма острых углов прямоугольного треугольника равна 90°.
∠В=90°-40°=50°
* * *
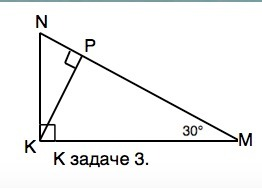
3) В прямоугольном треугольнике МКН угол К=90°, КР - высота. Гипотенуза MN=36, угол M=30°, Найти проекции катетов на гипотенузу.
----
Катет KN противолежит углу 30° и по свойству такого катета равен половине гипотенузы.
КN=18.
Сумма острых углов прямоугольного треугольника 90°.
Угол N=90°-30°=60°
В прямоугольном треугольнике КNP угол NKP=90°-60°=30°
NP противолежит углу 30° ⇒ равен половине NK ⇒ NP=9.
⇒ МР=36-9=27.
* * *
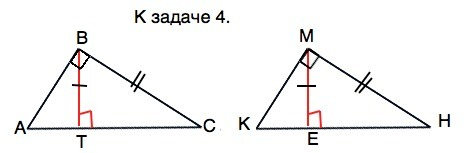
4). Докажите равенство прямоугольных треугольников по катету и высоте, опущенной на гипотенузу.
Рассмотрим прямоугольные ∆ ВТС и ∆ МЕН.
В них равные катеты являются гипотенузами.
Пусть ВТ=МЕ=а, . ВС=МН=b ,⇒ cos∠TBC=a/b, cos∠EMH=a/b. ⇒
∠ТВС=∠ЕМН. ⇒
∆ ВТС и ∆ МЕН равны по двум сторонам и углу между ними.
Тогда ∠ВСА=∠МНК, и в ∆ АВС и ∆ КМН имеется по равному катету и прилежащему острому углу.
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны. Доказано.
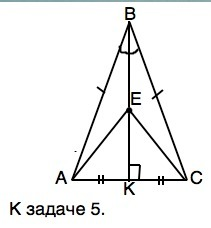
5).
В равнобедренном треугольнике АВС с основанием АС на медиане ВЕ отмечена точка Е. Докажите, что треугольник АЕС - равнобедренный.
В равнобедренном треугольнике медиана, проведенная к основанию, является ещё высотой и биссектрисой.⇒
∠АВЕ=∠СВЕ.
Рассмотрим ∆ АВЕ и ∆ СВЕ.
АВ=ВС по условию, ВЕ - общая сторона, углы между равными сторонами равны (ВК - биссектриса). ⇒
∆ АВЕ=∆ СВЕ по первому признаку равенства треугольников.
Из ∆ АВЕ=∆ СВЕ следует равенство АЕ=СЕ, и
∆ АЕС - равнобедренный. Доказано.