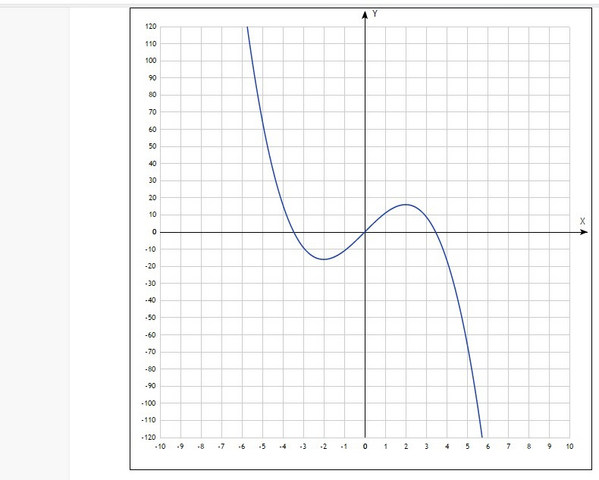
У=-х³+12х
1) точки пересечения с осью х
решаем уравнение
-х³+12х=0
х₁=0
х₂=2√3
х₃=-2√3
(0; 0), (2√3; 0), (-2√3; 0)
точки пересечения с осью у
х=0
у=0
(0; 0)
2) экстремумы
у'=-3x²+12
решаем уравнение
-3x²+12=0
x₁=-2 y₁=-16
x₂=2 y₂=16
точка минимума (-2; -16)
точка максимума (2; 16)
3) интервалы убывания и возрастания
убывание х∈[-2; 2]
возрастание х∈(-∞; -2]∪[2;+∞)
4) точки перегибов
у''=-6x
x=0
y=0
(0;0)
5) интервалы выпуклости и вогнутости
вогнутость х∈(-∞;0]
выпуклость х∈[0; +∞)
6) горизонтальные асимптоты
lim(-x³+12x)=+∞
x→-∞
горизонтальной асимптоты слева не существует
lim(-x³+12x)=-∞
x→+∞
горизонтальной асимптоты справа не существует
7) наклонные асимптоты
lim[1/x(-x³+12x)]=-∞
x→-∞
наклонной асимптоты слева не существует
lim[1/x(-x³+12x)]=-∞
x→+∞
наклонной асимптоты справа не существует
8) четность и нечетность функции
у=у(-х)
-х³+12х=х³-12х неверно
у=у(х)
-х³+12х=-х³-(-12х) верно, функция нечетная