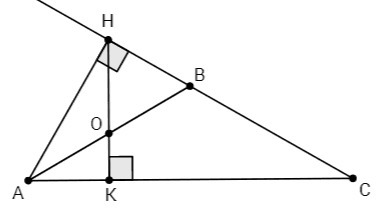
В равнобедренном треугольнике острым может быть только угол при вершине, противолежащей основанию (в треугольнике не может быть двух тупых углов).
∠ABH=60°
Внешний угол при вершине, противолежащей основанию равнобедренного треугольника, в два раза больше угла при основании.
∠BAC=∠BCA=30°
△AOK~△CHK (прямоугольные т. с равными острыми углами)
CH/AO=CK/AK
Высота, проведенная из вершины прямого угла, делит гипотенузу на отрезки, равные отношению квадрата прилежащего катета к гипотенузе.
AK=AH^2/AC, CK=CH^2/AC
CK/AK= CH^2/AH^2
Катет, лежащий против угла 30°, равен половине гипотенузы.
AH=AC/2
CH= √(AC^2 -AC^2/4) = AC√3/2
CH/AH= √3
CH/AO= (CH/AH)^2 =3
ИЛИ
∠OHB=90-30=60 => △OHB равносторонний, HB=OH
∠OAH=90-60=30, AHO=90-60=30 => △OAH равнобедренный, AO=OH
AO=HB
CAB=OAH => AB - биссектриса ∠CAH.
Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению прилежащих сторон.
HB/BC = AH/AC = 1/2 <=> BC=2HB
HC/AO = (HB+2HB)/HB= 3