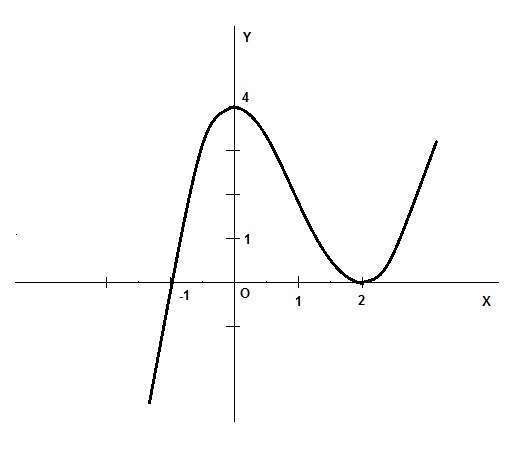
Y = x^3 - 3x^2 + 4
1) Обл. опред. D(X) = (-oo; +oo). Обл. значений E(Y) = (-oo; +oo).
2) Не четная, не нечетная, не периодическая.
3) Разрывов нет. Функция непрерывна на (-oo; +oo)
4) Точки пересечения с осями. С осью Oy: y(0) = 4. Точка A(0; 4)
С осью Ox: x^3 - 3x^2 + 4 = 0
y(-1) = -1 - 3 + 4 = 0 - точка B(-1; 0)
y(2) = 8 - 3*4 + 4 = 0 - точка С(2; 0)
5) Экстремумы. Производная равна 0.
y' = 3x^2 - 6x = 3x(x - 2) = 0
x1 = 0; y(0) = 4 - максимум.
x2 = 2; y(2) = 0 - минимум.
При x < 0 U x > 2 функция возрастает.
При 0 < x < 2 функция убывает.
6) Точки перегиба. Вторая производная равна 0.
y'' = 6x - 6 = 6(x - 1) = 0
x = 1; y(1) = 1 - 3 + 4 = 2
При x < 1 функция выпуклая вверх.
При x > 1 функция выпуклая вниз.
7) Асимптоты. Ни вертикальных, ни горизонтальных, ни наклонных нет.
8) График на рисунке.