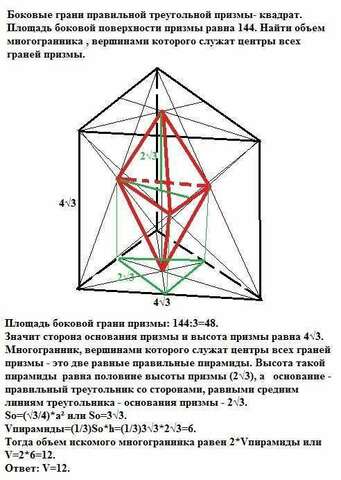
Площадь боковой грани призмы: 144:3=48 (три равных боковых грани).
Значит сторона основания призмы и высота призмы равна √48= 4√3.
Многогранник, вершинами которого служат центры всех граней призмы - это две равные правильные пирамиды. Высота одной такой пирамиды равна половине высоты призмы (2√3), а основание - правильный треугольник со сторонами, равными средним линиям треугольника - основания призмы - 2√3.
So=(√3/4)*a² или So=3√3.
Vпирамиды=(1/3)So*h=(1/3)3√3*2√3=6.
Тогда объем искомого многогранника равен 2*Vпирамиды или
V=2*6=12.
Ответ: V=12.