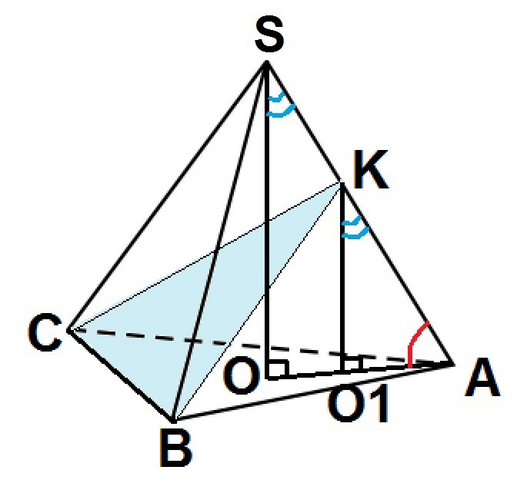
Пусть SABC - треугольная пирамида. Плоскость проходит через сторону BC основания этой пирамиды и пересекает противоположное боковое ребро AS в точке K так, что SK : AK = 3 : 4.
Треугольник BCK - сечение пирамиды SABC плоскостью, которая разбивает пирамиду SABC на две пирамиды - SKBC и KABC.
Объем пирамиды SABC:
V₁ = 1/3 * Sосн₁ * h₁
где Sосн₁ - площадь треугольника, лежащего в основании данной пирамиды, т.е. S(ABC)
h₁ - высота пирамиды SABC, т.е. перпендикуляр SO, проведенный к плоскости основания данной пирамиды
Объем пирамиды KABC:
V₂ = 1/3 * Sосн₂ * h₂
где Sосн₂ - площадь треугольника, лежащего в основании данной пирамиды, т.е. S(ABC) ⇒ Sосн₁ = Sосн₂
h₂ - высота пирамиды KABC, т.е. перпендикуляр KO₁, проведенный к плоскости основания данной пирамиды
Треугольники SOA и KO₁A подобны по двум углам:
∠KAO₁ = ∠SAO (угол наклона ребра к плоскости ABC)
∠SOA = KO₁A = 90°
⇒ стороны данных треугольников пропорциональны.
Поскольку SK : AK = 3 : 4, отрезок SK составляет 3 части, отрезок AK составляет 4 части, AS составляет 7 частей.
⇒ AK : AS = 4 : 7
⇒ KO₁ : SO = 4 : 7
⇒ h₂ : h₁ = 4 : 7
7h₂ = 4h₁
h₂ = 4h₁ / 7
V₁ 1/3 * Sосн₁ * h₁
---------- = -----------------------------
V₂ 1/3 * Sосн₂ * h₂
V₁ S(ABC) * h₁
----------- = -----------------------
V₂ S(ABC) * h₂
V₁ h₁
--------- = -----------
V₂ h₂
V₁ h₁
---------- = -----------------
V₂ 4h₁ / 7
35 7
--------- = ---------
V₂ 4
35 * 4 = 7V₂
V₂ = 20 (куб. ед.)
20 составляет бОльшую часть от 35 ⇒ это и есть бОльший из объемов, на которые плоскость разбивает исходную пирамиду.