Рассмотрите такое решение:
1) По условию 4-значное число содержит все представленные цифры (2, 3, 4 и 5). Поэтому количество таких четырёхзначных чисел определяется числом размещений, то есть Р=х!=4!=24.
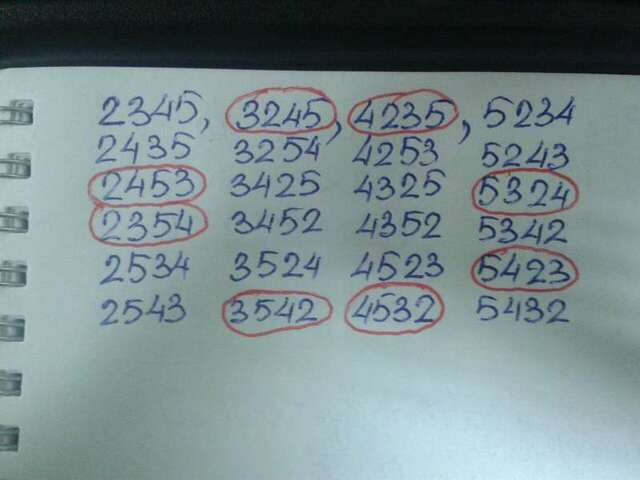
2) Так как таких чисел немного, то можно рассмотреть делимость на 11 каждого из них (числа во вложении).
3) Согласно признаку делимости на 11 сумма 2, 3, 4 и 5 даёт число 14, то есть при попарном разбиении не будет такой комбинации, которая даёт в разности число, кратное 11 (кроме 0), но зато 2+5=4+3 (а также 5+2=4+3, 5+2=3+4, 2+5=3+4, а также 3+4=2+5, 4+3=2+5, 4+3=5+2 и 3+4=5+2) - эти восемь комбинаций на нечетных и чётных местах указывают числа, которые кратны 11 согласно признаку делимости на 11. То есть, эти числа такие: 2453, 2354, 3245, 3542, 4235, 4532, 5324 и 5432.
Ответ: таких чисел 8.
P. S. Во вложении указаны все 24 числа и те, которые обведены уветным - есть искомые.