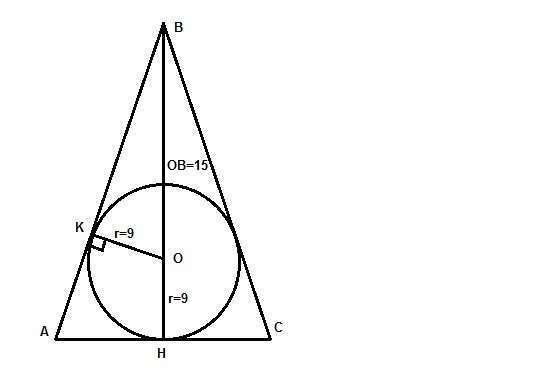
Вот рисунок. По условию OK = OH = r = 9; OB = 15.
Радиус в точке касания перпендикулярен касательной, поэтому OKB = 90°.
По теореме Пифагора KB^2 = OB^2 - OK^2 = 225 - 81 = 144; KB = 12.
По свойству двух касательных из одной точки, AK = AH = x.
Опять же по теореме Пифагора
AH^2 + BH^2 = AB^2 = (AK + KB)^2
x^2 + (15 + 9)^2 = (x + 12)^2
x^2 + 24^2 = x^2 + 24x + 12^2
24^2 - 12*2*6 = 24x
x = (24^2 - 24*6)/24 = 24 - 6 = 18
Основание a = 2*AH = 2x = 2*18 = 36, высота h = BH = 15+9 = 24
Площадь S = a*h/2 = 36*24/2 = 36*12 = 3*12*12 = 432.
Посчитано в уме, без калькулятора!