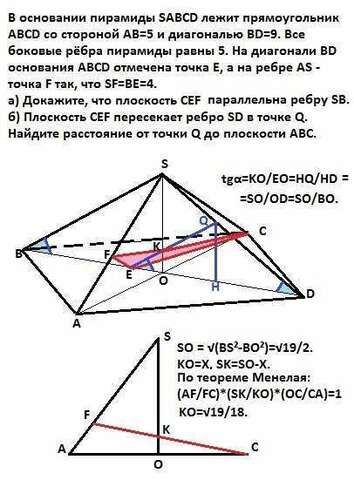
А). Высота пирамиды по Пифагору:
SO=√(SB²-BO²) = √(25-81/4) =√19/2.Рассмотрим треугольник ASO и
секущую FC в нем. По теореме Менелая имеем:(AF/FS)*(SK/KO)*(OC/CA)=1.
Подставим имеющиеся значения, приняв отрезок ОК за Х:
(1/4)*((√19/2-Х)/Х)*(1/2)=1. Отсюда Х=√19/18.
Заметим, что точка К - пересечение прямых FC и SO.
Итак, КО=√19/18. Тогда в треугольнике КЕО:
tg(В треугольнике OSD тангенс угла SDO:
tg(SDO)=SO/OD или tg(SDO)=(√19/2)/(9/2)=√19/9.
Итак, в треугольнике EQD углы QED и QDO при основании равны,
a Следовательно, треугольники ВSD и EQD подобны и EQ параллельна BS. Прямая EQ принадлежит плоскости CEF, значит плоскость CEFпараллельна ребру BS, что и требовалось доказать.
б). Треугольники ВSD и EQD подобны (доказано выше), поэтомуEQ/BS=DE/DB, отсюда EQ=BS*DE/DB или EQ=5*5/9=25/9.Тогда в равнобедренном треугольнике EQD высота QH=√(EQ²-(OD/2)²) или QH=√475/18=5√19/18 ≈ 1,2.